Published 2023. 8. 20. 16:25
반응형
LIS 란?
- Longest Increasing Subsequence
- ex) 수열 A = {10, 20, 10, 30, 20, 50}가 주어지고 가장 긴 증가하는 부분 수열을 구하는 문제
- 증가하는 부분 수열을 모두 구해보면 아래와 같음
- {10}, {20}, {30}, {50}
- {10, 20}, {10, 30}, {20, 30}, {20, 50}, {30, 50}
- {10, 20, 30}, {10, 20, 50}, {10, 30, 50}, {20, 30, 50}
- {10, 20, 30, 50}
- 이 중 가장 길이가 긴 부분 수열은 {10, 20, 30, 50}
- 증가하는 부분 수열을 모두 구해보면 아래와 같음
해결 방법 1 - O(n^2)
- 가장 쉬운 해결 방법은 일반적인 dp를 사용하는 방법
- dp[i] = dp[i - 1]과 arr[i]를 포함시켜 만들 수 있는 가장 긴 증가하는 부분수열을 비교하여 더 큰 값을 넣어주면 됨
- arr[i]를 포함시켜 만들 수 있는 가장 긴 증가하는 부분수열을 구하는 방법은 arr[0] ~ arr[i - 1] 중 arr[i]보다 값이 작으면서 dp의 해당 index의 값이 가장 큰 값 + 1
- ex) arr[] = {10, 20, 10, 30, 20, 50}이 주어졌을 때
- dp[0] = 1 (10을 넣는 방법)
- dp[1] = 2 (10, 20을 넣는 방법), 1 (dp[0]) 중 큰 값 = 2
- dp[2] = 1 (10을 넣는 방법), 2 (dp[1]) 중 큰 값 = 2
- dp[3] = 3 (10, 20, 30을 넣는 방법), 2 (dp[2]) 중 큰 값 = 3
- dp[4] = 2 (10, 20을 넣는 방법), 3 (dp[3]) 중 큰 값 = 3
- dp[5] = 4 (10, 20, 30, 50)을 넣는 방법, 3 (dp[4]) 중 큰 값 = 4
- 정답 = 4
해결 방법 2 - O(nlogn)
- 해결 방법 1은 이해하기도 쉽고 구현하기도 쉽지만 arr[i]를 포함시켜 만들 수 있는 가장 긴 증가하는 부분수열을 구하기 위해선 0 ~ i-1의 반복문이 필요함
- 시간 복잡도가 n^2
- 더 빠르게 찾기 위해서 arr[i]를 포함시켜 만들 수 있는 가장 긴 증가하는 부분수열을 구하는 시간을 줄여보자
- dp + 이분 탐색을 활용
- arr[] = {10, 20, 9, 30, 20, 50}이 주어졌다고 가정
- List 타입의 dp에 0 삽입 (arr의 각각의 값이 1 이상이기 때문)
- i = 0일 때, List 타입의 dp에 arr[0] 삽입

- i = 1일 때, dp의 마지막 숫자(10)가 arr[i](20)보다 작다면 삽입

- i = 2일 때, dp의 마지막 숫자(20)이 arr[i](9)보다 크거나 같음
- 이런 경우에는 이분 탐색을 통해 dp에서 9보다 작은 값 중에서 최대값을 찾음(0)
- 0 뒤에 9 삽입

- 현재 dp에는 9, 20이 들어있지만 이는 {9, 20}이 가장 긴 증가하는 부분수열이라는 뜻이 아닌 길이가 2가 최대라는 의미
- 이후에 10이 나온다면 9 뒤에 10을 넣음으로써 {9, 10}으로 만들 수 있기 때문에 위와 같은 작업을 한 것임
- i = 3일 때, dp의 마지막 숫자(20)이 arr[i](30)보다 작기 때문에 삽입

- i = 4일 때, dp의 마지막 숫자(30)이 arr[i](20)보다 크거나 같기 때문에 9 뒤에 20 삽입

- i = 5일 때, dp의 마지막 숫자(30)이 arr[i](50)보다 작기 때문에 삽입
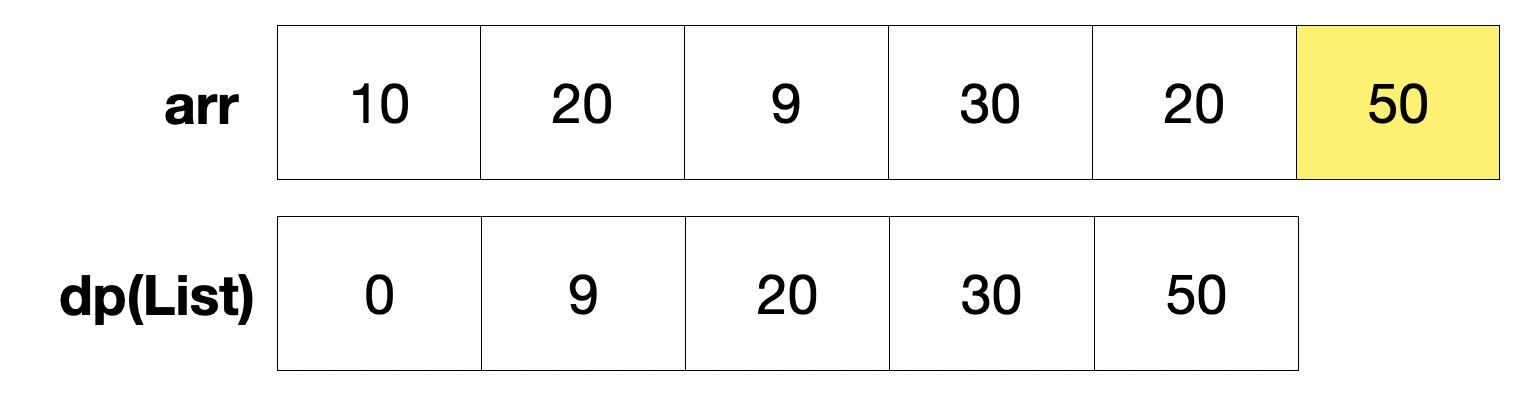
- dp의 길이 - 1(첫번째 0 제외) = 4가 정답, 이 때 {9, 20, 30, 50}이 가장 긴 증가하는 부분수열은 아님
구현
코드
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class p12015 {
static List<Integer> dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] arr = new int[n];
for (int i = 0 ; i < n ; i ++) {
arr[i] = sc.nextInt();
}
dp = new ArrayList<>();
dp.add(0);
dp.add(arr[0]);
for (int i = 1 ; i < n ; i ++) {
if (arr[i] > dp.get(dp.size() - 1)) {
dp.add(arr[i]);
} else {
// dp에서 arr[i]보다 작은값 중 가장 큰 값 바로 뒤의 값을 arr[i]로 수정
// arr[i]보다 작은값 중 가장 큰 값을 찾기 위해 이분 탐색 사용
binary_search(arr[i]);
}
}
System.out.println(dp.size() - 1);
}
private static void binary_search(int x) {
int left = 0;
int right = dp.size() - 1;
int mid = 0;
while (left <= right) {
mid = (left + right) / 2;
if (dp.get(mid) >= x) {
right = mid - 1;
} else {
if (dp.get(mid) < x && dp.get(mid + 1) >= x) {
break;
} else {
left = mid + 1;
}
}
}
dp.set(mid + 1, x);
}
}반응형
'JAVA > 알고리즘 개념 정리' 카테고리의 다른 글
| [JAVA] Knapsack 알고리즘 (0) | 2022.10.11 |
|---|---|
| [JAVA] CCW (0) | 2022.06.17 |
| [JAVA] 외판원 순회 문제 (TSP) + 시간초과 해결방법 (3) | 2022.06.16 |
| [JAVA] 세그먼트 트리 (Segment Tree) (0) | 2022.06.09 |
| [JAVA] Union-Find (0) | 2022.06.06 |